Nanocomposites: Multiscale Modeling
Pertinent to our extensive efforts in the experimental side, which include the development of synthesis and fabrication techniques for treated nanoparticles and their polymer nanocomposites and the development of novel characterization techniques that enable the direct probing of the in situ properties of the interphase, considerable effort has been devoted to the development of a multiscale modeling method that explicitly includes the interphase and in situ nanoparticle morphology to ensure accurate prediction and design of nanocomposites (see Figure 1). This method, coupling finite element method and micromechanics, and molecular dynamics calculation or even nanoscale experimental results, operates at relatively low computational cost and is highly accessible.
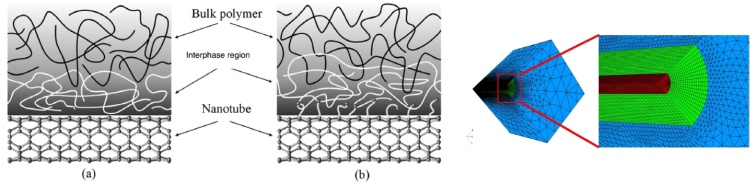
Our hybrid modeling technique presents a clear hierarchy, as shown in Figure 2. First, the properties of the constituent materials, matrix, interphase and nanoinclusions, can be either directly measured or calculated by small-scale molecular dynamics simulation. We then establish a finite element unit cell model consisting of a nanoparticle encapsulated in one or more layers of surrounding interphase, embedded in the bulk matrix material. In this step, the bulk matrix must be large enough so that the inhomogeneities, which are nanoparticle and interphase, see the matrix as infinite. The in situ configuration of the nanoparticle and the interphase can be explicitly included in this unit cell. We then apply appropriate boundary conditions and solve for the strain field inside the interphase(s) and the nanoparticle. The numerical dilute strain concentration tensors of each phase can then be calculated. Using these as inputs, the final step is to employ the Mori-Tanaka method to solve for the mechanical response of the polymer nanocomposite for an array of interacting inclusions. This entire calculation is done in the viscoelastic domain so that time and temperature effects are studied.

Temperature sweeps in dynamic mechanical (DMA) response show that the glassy state storage modulus of modified SWCNT /PMMA composites are significantly higher than that of the neat polymer. The strong influence of the interfacial region is clearly evident from the glass transition temperature (Tg) shift, as shown in Figure 2 where tan d is plotted against temperature for functionalized SWCNT/PMMA composites. In frequency domain time-temperature superposition can be used to show differences between the viscoelastic behavior of nanocomposites and the parent polymer system.
Publications:
H. Liu, T. Ramanathan, L.C. Brinson, Controlling and Modeling the Interphase in Polymeric Nanocomposites, manuscript in preparation, 2007.
H. Liu, L.C. Brinson, Reinforcing Efficiency of Nanoparticles: A Simple Comparison for Polymer Nanocomposites, submitted, Composite Science and Technology, 2007.
H. Liu, L.C. Brinson, A Hybrid Numerical-Analytical Method for Modeling the Viscoelastic Properties of the Polymeric Nanocomposites, Journal of Applied Mechanics, vol. 73, 758-768 (2006).
R. D. Bradshaw, Fisher, F. T., L. C. Brinson. Fiber Waviness in Nanotube-Reinforced Polymer Composites: II. Modeling Via Numerical Approximation of the Dilute Strain Concentration Tensor, Composites Science and Technology, 63 (11): pp. 1705-1722 (2003).
Fisher, F. T., R. D. Bradshaw, L. C. Brinson. Effects of Nanotube Waviness on the Mechanical Properties of Nanoreinforced Polymers. Applied Physics Letters, vol 80, no. 24, pp. 4647-4649, (2002).