FEA simulation is a powerful tool for understanding structure-property relationships in polymer nanocomposites (PNCs). However, FEA simulation is known to be expensive, both monetarily and computationally, when investigating materials with complex microstructural morphologies. The existence of an interphase with often significantly modified properties within the polymer regions near interfaces adds further computational cost.
We have previously found that models explicitly modeling the interphase in FEA simulations as a distinct phase with properties found by simple transformations of those of the neat polymer (e.g. shifting and broadening of the matrix viscoelastic (VE) response in frequency space) reduces computational cost while more accurately reflecting experimental observations [1]. Furthermore, our previous group members developed a CNN (convolutional neural network) model as a surrogate for FEA simulation to predict several scalar VE properties like glassy modulus, rubbery modulus, and tan delta peak[2].
Ongoing work seeks to open a new realm for the surrogate model development in the PNC VE field. Since FEA simulation generates the full master curve of the PNC, a strong surrogate model should be able to use the same inputs of FEA simulation and generate the same outputs, namely the master curve of the PNC. Once we obtain the master curve, we automatically obtain the previously mentioned scalar VE properties since they are specific points on the curve.
We are currently developing a deep NN (neural network) that takes microstructure images, master curves of polymer matrices, shifting factors, and broadening factors as inputs, and generates storage modulus and tan delta curves as output. The NN model has CNN embedding layers connected to MLP (multi-layer perceptron) layers.
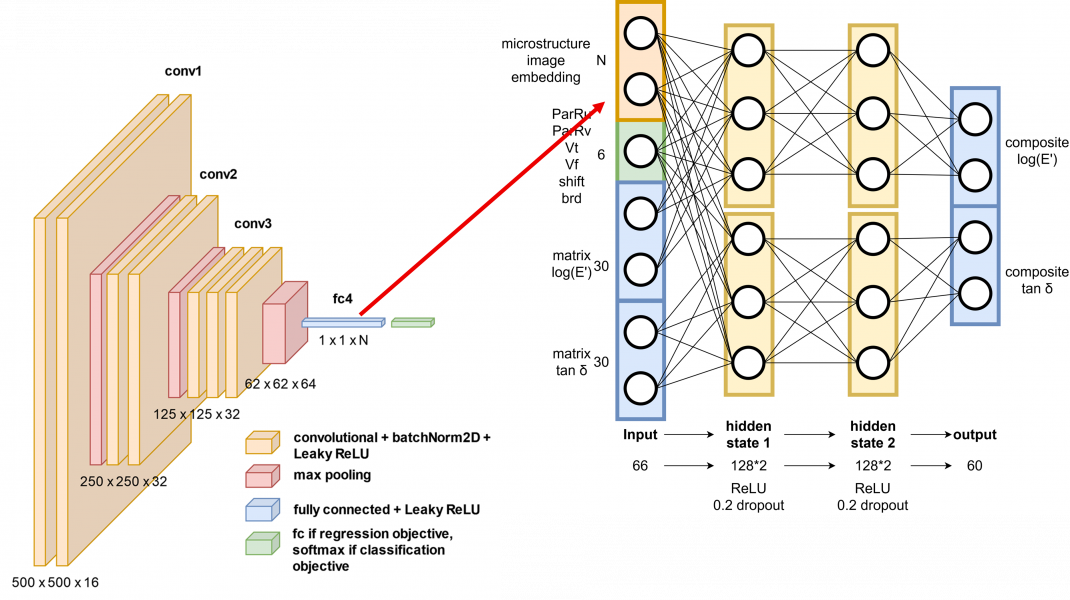
The results shown below show promising performance. Meanwhile, training the NN without the CNN embedding takes less than an hour without GPU. The inference process takes less than 1 second, while an FEA simulation for the same microstructure takes 6 minutes on 8 CPU cores, making a roughly 400x reduction in computational cost.

Active Researcher on the Project:
Relevant Publications
[1] Wang, Yixing, et al. "Identifying interphase properties in polymer nanocomposites using adaptive optimization." Composites Science and Technology 162 (2018): 146-155.
[2] Wang, Yixing, et al. "Mining structure–property relationships in polymer nanocomposites using data driven finite element analysis and multi-task convolutional neural networks." Molecular Systems Design & Engineering 5.5 (2020): 962-975.