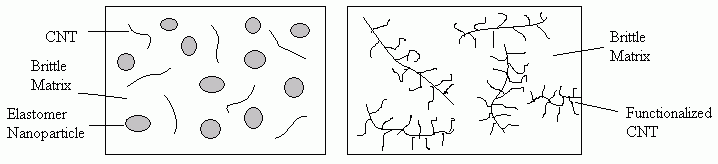
Epoxy materials span a wide range of applications, from sporting equipment to structural components in the automotive and aerospace industries. It has been known for two decades that dispersing a second elastomer (or rubber) phase into an epoxy matrix can result in dramatic fracture toughness improvements. However, the ductility imparted by the rubbery phase typically results in a concurrent decrease in the material’s modulus, or stiffness. Carbon nanotubes – with strengths on the order of 1 TPa – are seen as very promising candidates as nanofillers for simultaneously improving both the stiffness and toughness of rubber-toughened epoxy materials. As such, various systems involving the efficient dispersion of both rubber particles and carbon nanotubes are being tested in order to obtain the optimal balance between toughness and stiffness. Figure 1 shows two such systems in which a) nanotubes and rubber nanoparticles are separately dispersed in an epoxy matrix, and b) nanotubes functionalized with elastomer brushes are dispersed in order to further improve the interfacial interaction between the nanotubes and matrix.

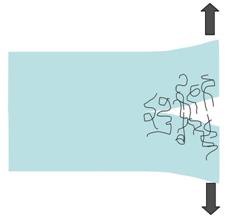
In nanoreinforced polymers, nanotubes are typically curved and entangled in situ (Fig. 2). This is in stark contrast to traditional composites (both short and continuous fiber) in which fibers are straight and often aligned. This nanoparticle morphology will greatly impact thermomechanical properties of these systems. While the origins of increased stiffness of nanocomposites are beginning to be well understood, including the effect of fiber curvature or waviness, the origins of toughness and strength in nanocomposites and the relation of these properties to the nanoparticle architecture and in situ morphology and connectivity has yet to be examined. For instance, curved, entangled nanotubes bridging a crack in DCB test shown in Fig. 3 may provide toughening mechanisms. Thus, our goal is to take into account the phenomenon of nanotube curvature and entanglement and to examine its effect on the critical properties of toughness and strength in nanocomposites. The results will be useful for the design of nanoreinforced polymers which have optimized thermomechanical properties.
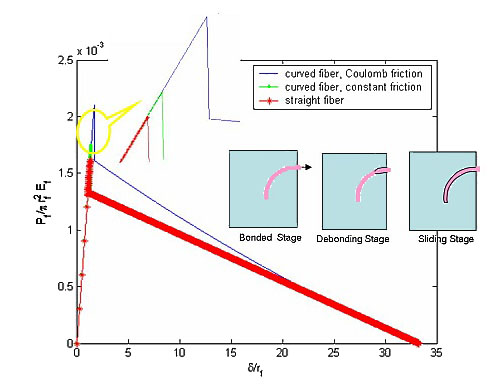
To model fracture toughness of nanocomposites in this context, we begin with the classic shear-lag model for pullout of a single straight fiber embedded in a matrix and modified it to account for a curved architecture. The complete force-displacement curve for single curved fiber pullout has been derived, including bonded fiber/matrix, debonding and sliding stages. In our simulations, different from a straight fiber model, we use a Coulomb friction assumption for the interfacial stress to account for the influence of the curvature on the normal force. Fig 4 shows sample force-displacement curve results for single curved fiber pullout, showing the difference from a straight fiber result. Based on this single curved fiber pullout result, we are now constructing the bridging law for crack bridging in nanocomposites, from which we will be able to predict toughness, strength, bridging zone size, critical stress for steady state matrix crack propagation.
Researchers on the Project:
Collaborators:
Irene Beyerlein
Linda Schadler
Publications:
Xinyu Chen, Irene J. Beyerlein, L. Catherine Brinson. "Curved-Fiber Pullout Model for Nanocomposites. Part 1: Bonded Stage Formulation." Mechanics of Materials 41.3 (2009): 279-292.
Xinyu Chen, Irene J. Beyerlein, L. Catherine Brinson. "Curved-Fiber Pullout Model for Nanocomposites. Part 2: Debonding and Sliding Stage Formulation." Mechanics of Materials 41.3 (2009): 293-307.